この片対数グラフの傾きと切片は何を表しているのですか Yahoo 知恵袋
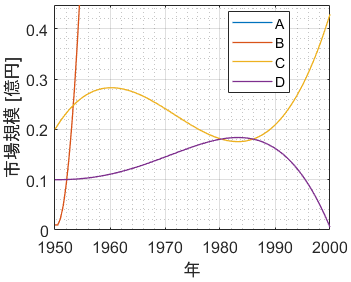
Python, numpy, matplotlib, 可視化, 科学技術計算 matplotlibのset_xscale とset_yscaleに'log'を指定することで片対数および両対数グラフを描くことができる。 例として y = e 2 x 1 をプロットする。270 付録A 測定値の取り扱いとグラフの描き方 所の副尺目盛を読む.副尺の1 目盛は005 mm であり,図では副尺目盛の9 番目(045 mm)が主尺の 目盛と一致している.最後に主尺目盛の数字と副尺の数字を足して145 = 1245 mm となる. ねじマイクロメータ
片対数グラフ 傾き 最小二乗法
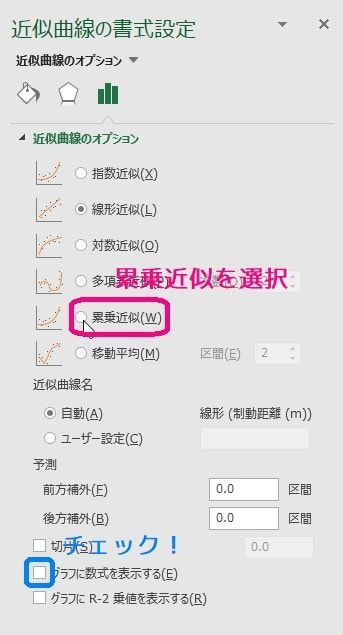
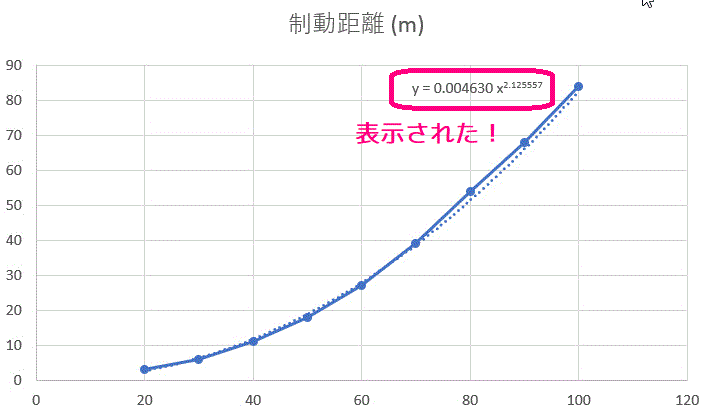
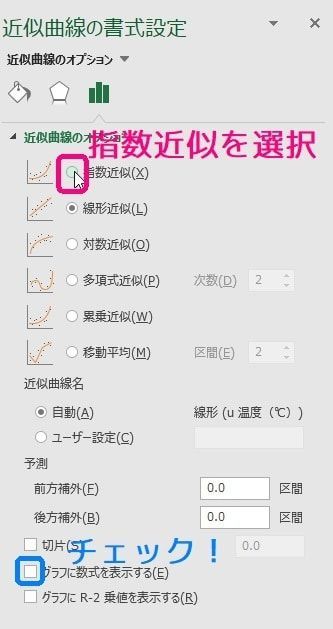
片対数グラフ 傾き 最小二乗法- このグラフからそれが読み取れるのは難しいですね。 ここ何日かで、日本の感染者数の増え方増えた(対数軸にした時の直線の傾きが大きくなった)ことがわかります。 片対数軸? こんな話を耳にして、算数・数学・統計の基礎知識の重要性を実感。累乗近似にチェックを入れると同時に、グラフに数式を表示するを選択しておくといいです。 すると、両対数グラフ上での直線近似ができるのです。 すると、yとxの乗が比例関係にあるのがわかります。 なお、上の直線の見かけ上の傾きはを
2
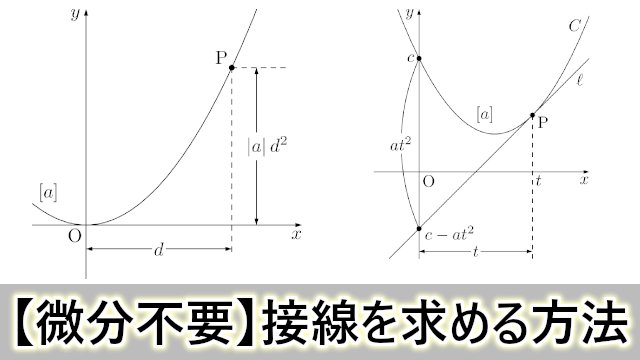
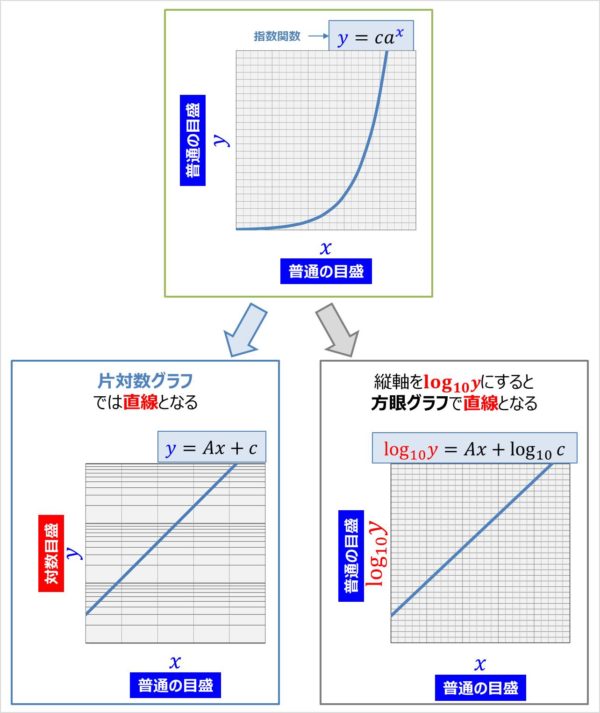
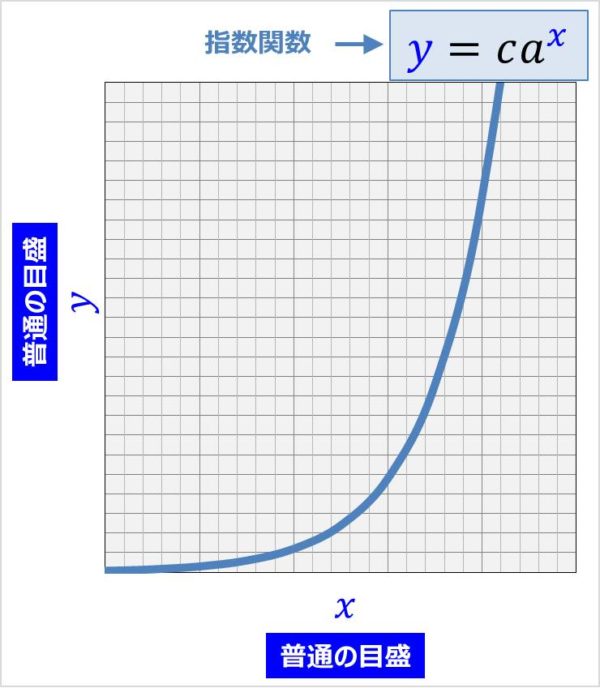
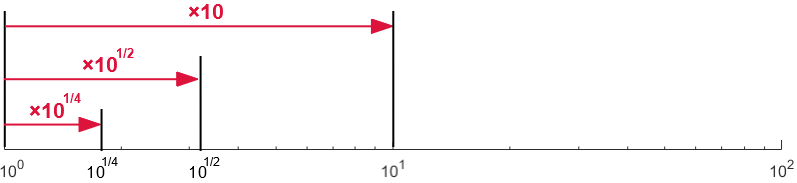
4 2 対数グラフ (19/2/6記) 対数プロットして直線状になったとして、 傾きを測る or 確認することがしばしば行われる。 真面目にやるならば1次回帰曲線を求めたりするのかもしれないが、 大まかに調べるために、脇に三角形を描く方法が最近は良く使わしかしながら対数をとってグラフを書くときだけはこの次元についての情報を一時的に捨て \ (ma=F\) を数値だけに関する無味乾燥な数学の方程式と見るのである。 単なる数学の方程式にくらべ物理の方程式は美しいと思う。 これはおそらく物理の方程式が指数関数 ( は正の定数、 は定数)の両辺の 常用対数 を取ると となる。 そこで横軸を通常の目盛りに、縦軸を対数目盛にすると、グラフが 直線 (傾き , y切片 の 一次関数 )になる。 利用例 編集 両対数グラフ 同様、乗数の値を決定するのに有効である。 化学 では アレニウスプロット によって 活性化エネルギー が求められる。 参考文献 編集 ^ David Carr Baird・加藤幸弘・千川道幸・近藤康
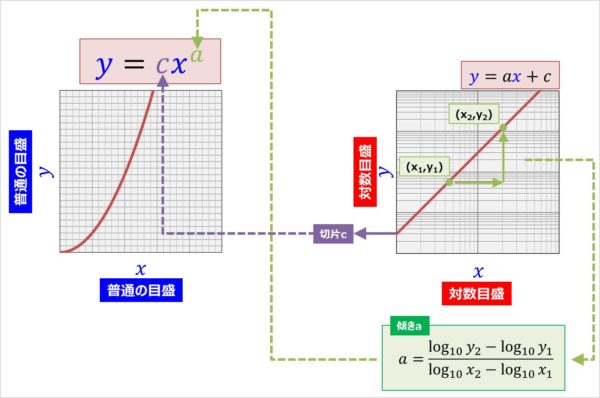
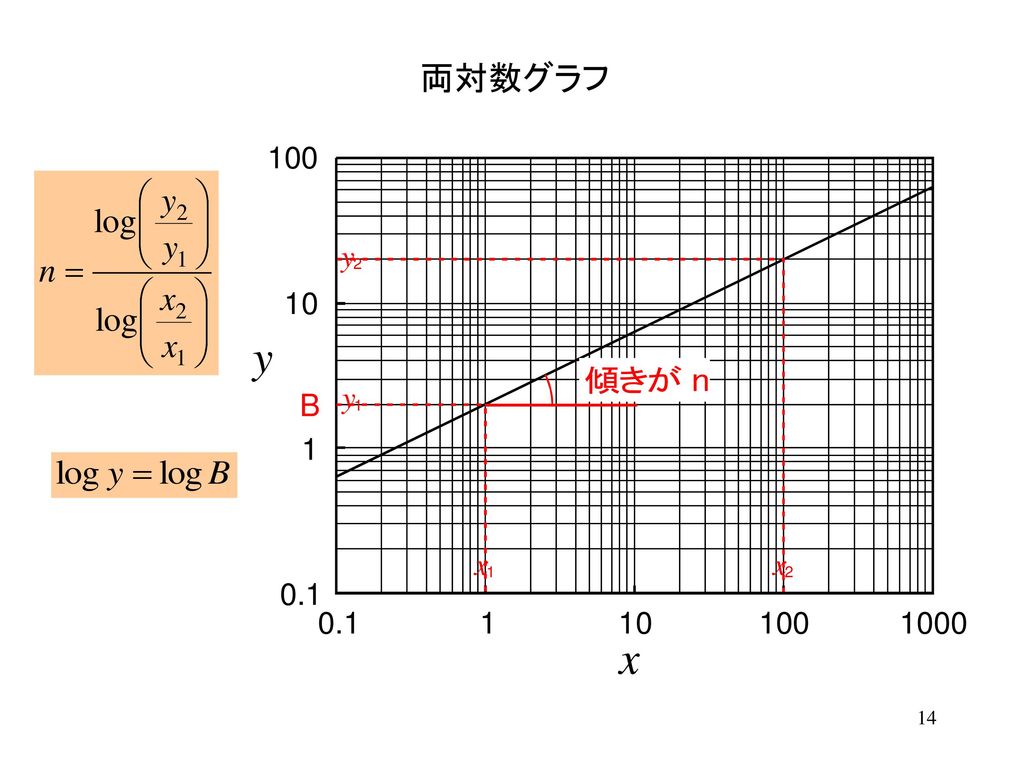
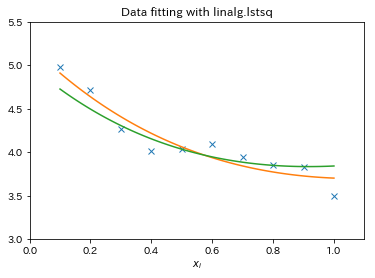
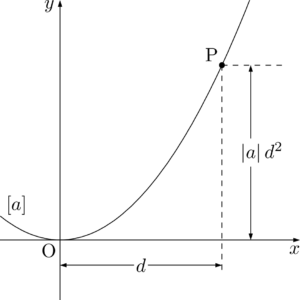
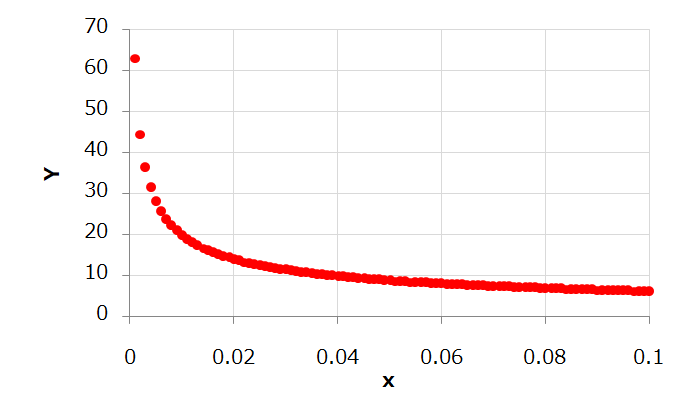
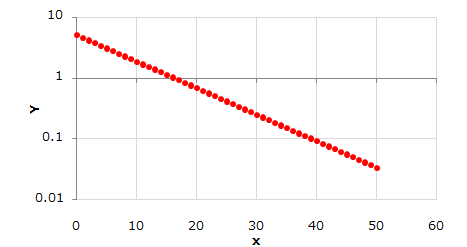
片対数グラフにおける回帰直線の求め方 指数関数的な増減をしそうなデータ の回帰直線を求める場合、 X = x, Y = log 10 y と置いてから最小2乗法を適用し、 Y = a X b の a, b の値を求めると回帰直線 y = 10 b ⋅ 10 a x と変形することができる。 4.両対数グラフについて ここでは、両対数グラフを使う実用例を1つ紹介したいと思います。 とはいっても、両対数グラフが役に立つ場面グラフを書いてみれば傾きと切片の意味がより深く理解できます。 傾き =変化の割合 = ( y の増加量)÷ ( x の増加量) = x が 1 増えたときの y の増分 切片 = x が 0 のときの y の値 = 点 B から原点 O までの距離 ( B が O より下にあるときは距離を − 1 片対数グラフの回帰直線をPythonで求めようとして少しハマったのでそのメモ。 仮想データを準備して、X軸を対数変換して回帰直線を求めた。 Dive into Data Science
片対数グラフ 傾き 最小二乗法のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  | |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 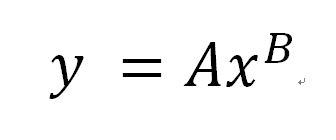 | |
 |  | |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
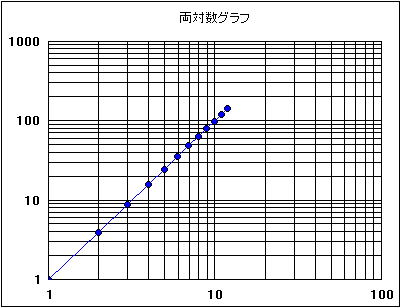 |  |
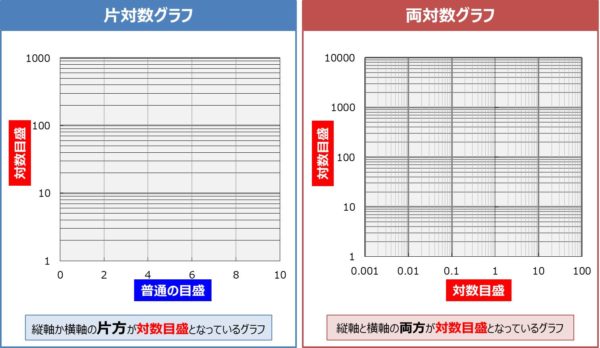
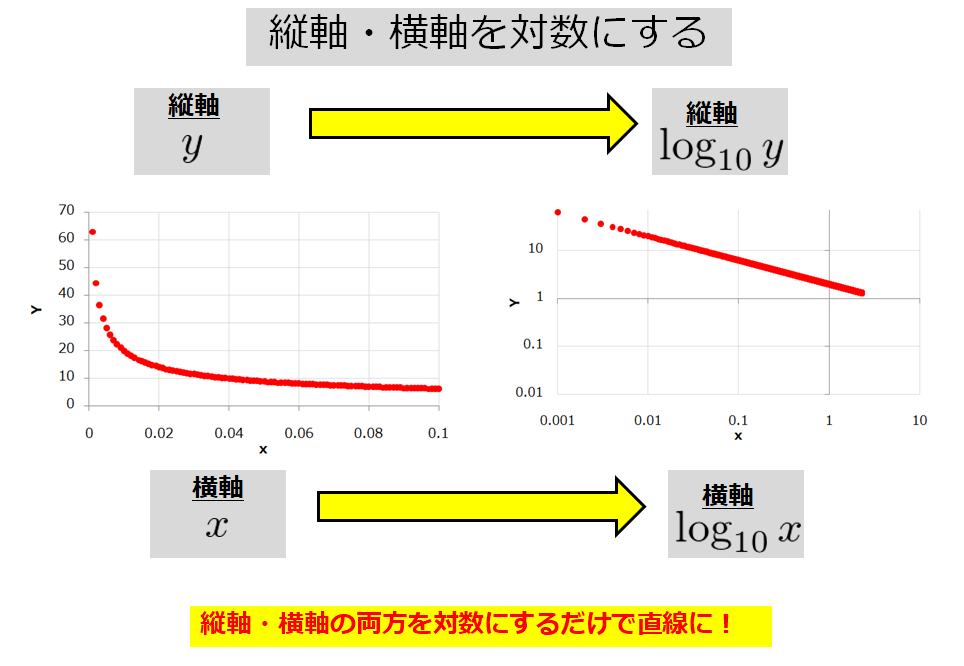
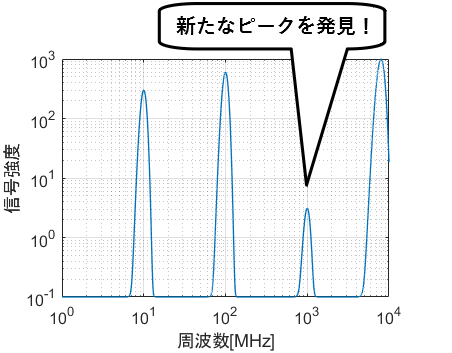
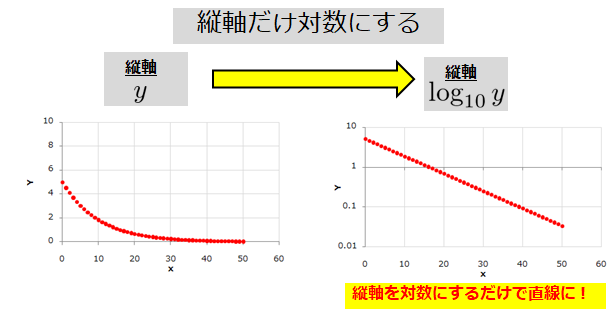
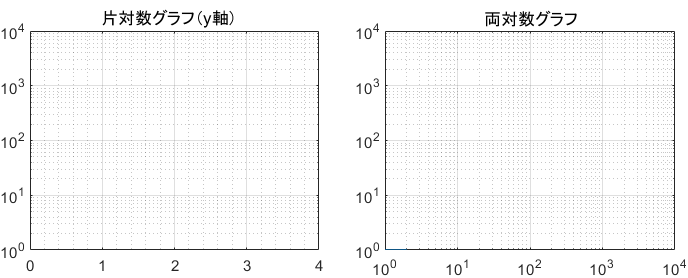
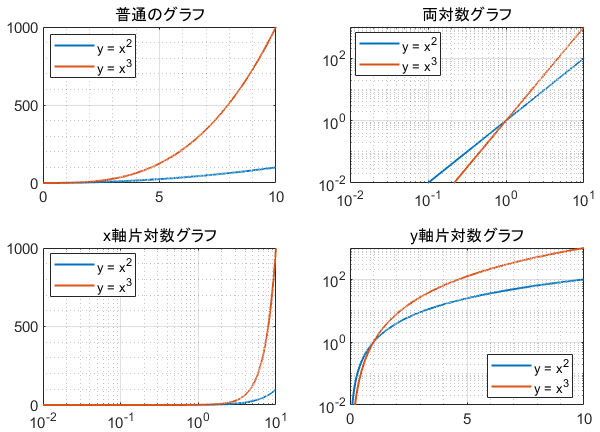
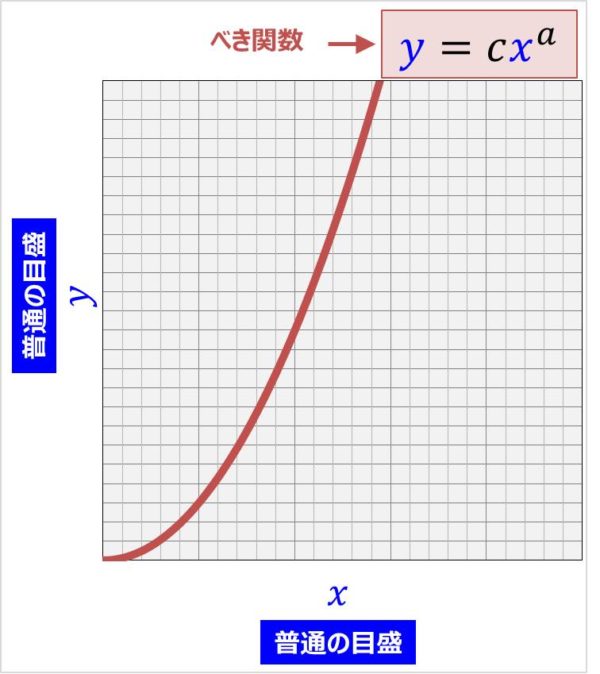
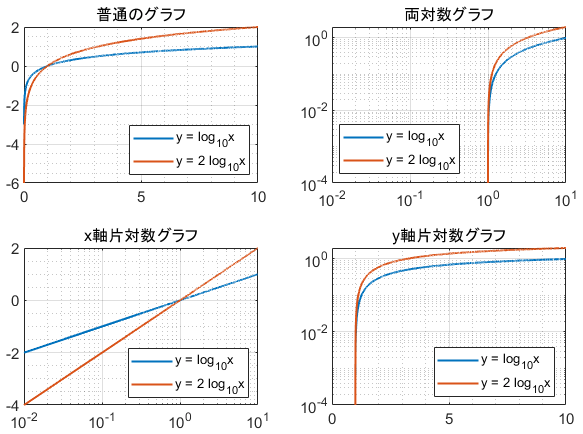
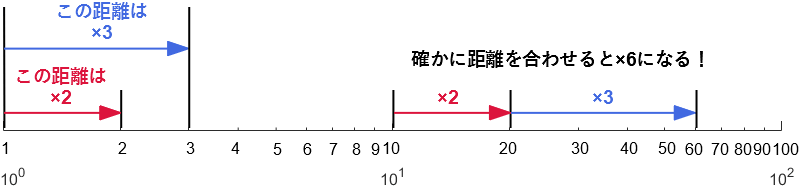
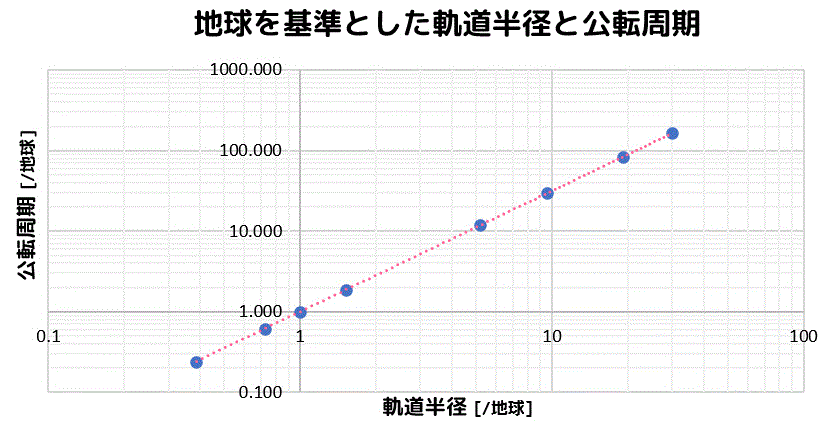
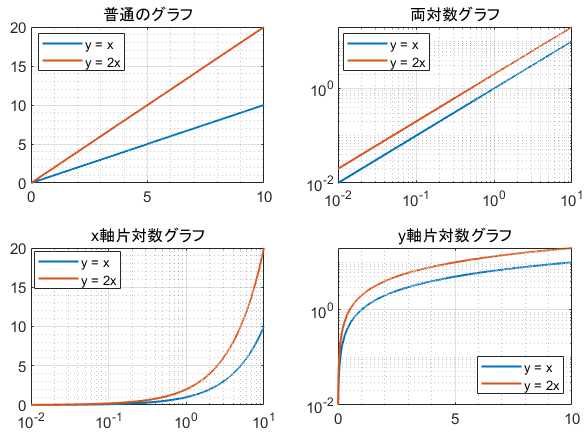
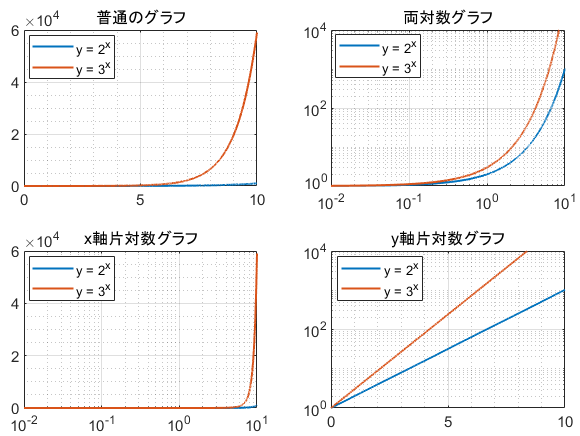
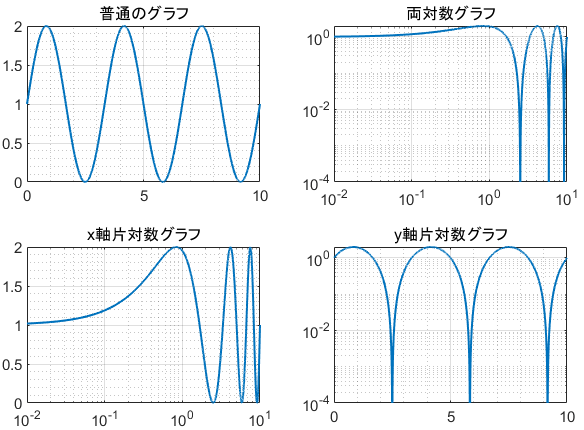
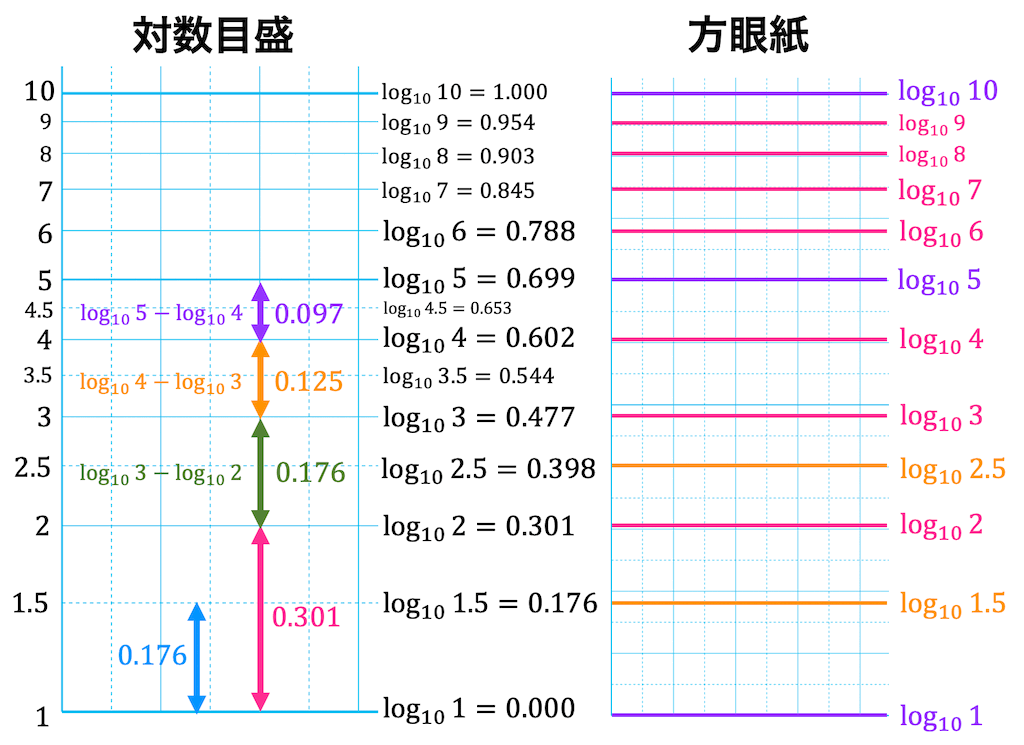
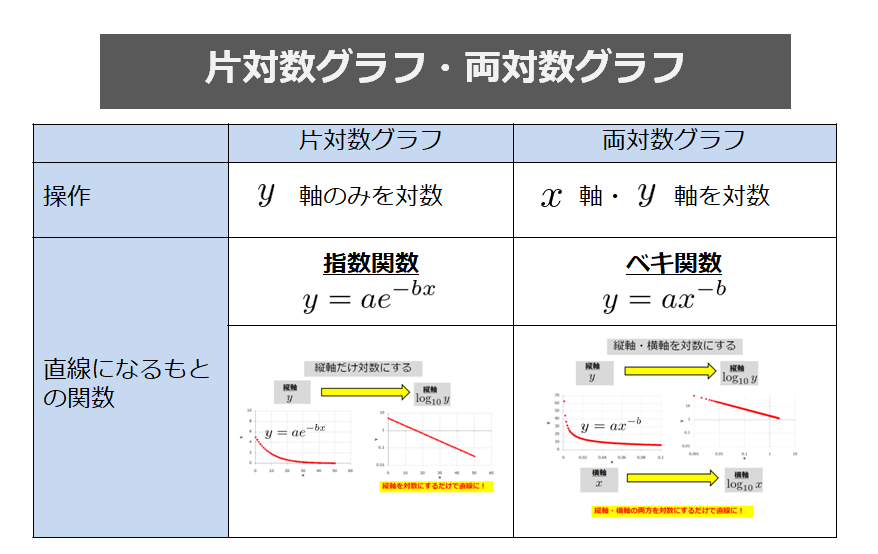
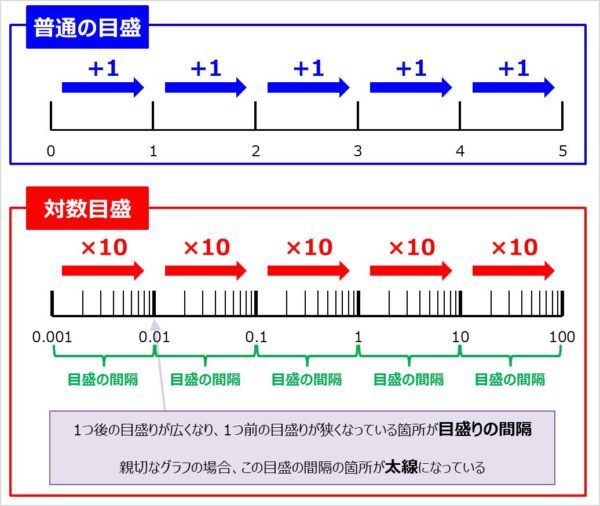
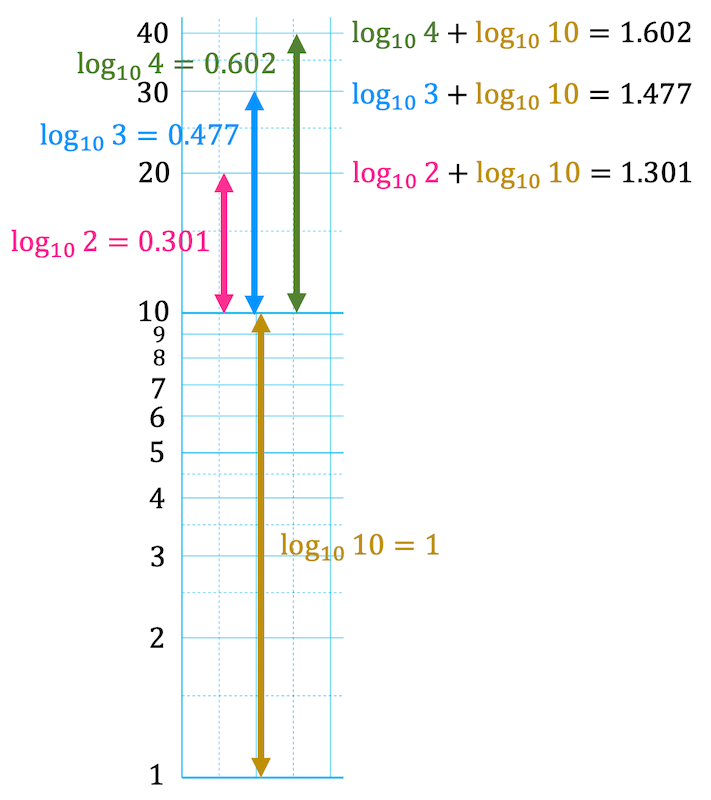
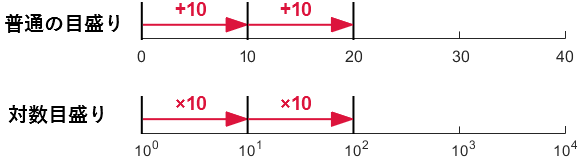
また、べき関数 の は両対数グラフにおける切片 と等しくなることも分かります。 また、直線 の2点, を結んだ時の傾きaは となります。 まとめ この記事では『片対数グラフ』と『両対数グラフ』について、以下の内容を説明しました。 当記事のまとめ 指数関数 は片対数グラフでは直線 になる 指数関数 の底 は で求めることができる 指数関数 の は片対数グラフにおける切片 と等しくなる べき関数一般的なグラフでは、目盛は「0,1,2,3」や「0,10,,30」のように一定距離ごとに一定数増えていきますが、対数目盛は「0,10,100」などのように、一定距離ごとに n 倍ずつ増えていきます そして、この対数目盛がx,y軸のどちらかのみに付いているものを 片
Incoming Term: 片対数グラフ 傾き, 片対数グラフ 傾き エクセル, 片対数グラフ 傾き 意味, 片対数グラフ 傾き 時定数, 片対数グラフ 傾き 単位, 片対数グラフ 傾き 求め方 エクセル, 片対数グラフ 傾き 最小二乗法,




0 件のコメント:
コメントを投稿